Git
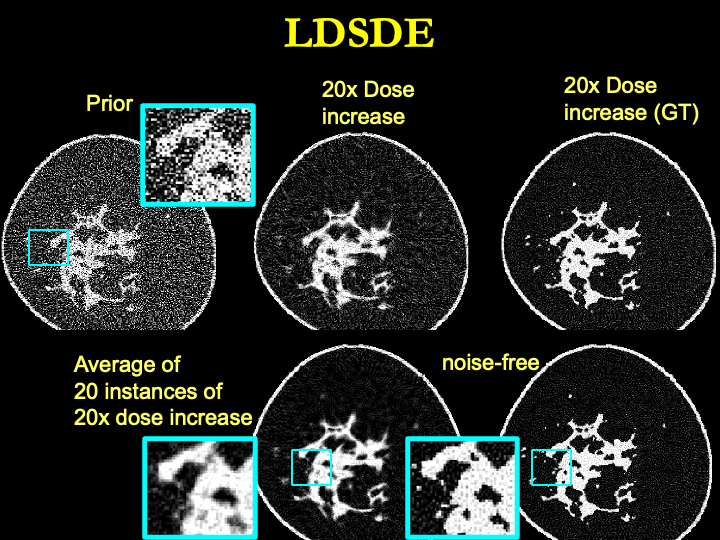
Low-Dose continioues SDE, or LDSDE for short, formulates low-dose to high-dose (qunatum-noise-wise) breast CT image synthesis problem into standard continous SDE problem suitable for diffusion network. Detailed derivation has been shown below
Low-Dose Continous SDE
Sampling
Suppose we have a perfect projection without any noise, $\pmb x_{-1}$, which is also normalized, we can get initial ($t=0$) high-dose scan and prior ($t=1$) low-dose scan using the simple addition of quantum and electronic noise. [All projections are normalized by $I_0$, the high dose]
\(\text{denote }\pmb\sigma^2_q = \frac{\pmb x_{-1}}{I_0}
\\
\pmb x_0 \sim \pmb{\mathcal{N}}\left(\pmb x_{-1},\pmb\sigma^2_q + \sigma_e ^2\right)
\\
\pmb x_0 = \pmb x_{-1} + \sqrt{\pmb\sigma^2_q + \sigma_e ^2} \pmb\epsilon
\\
\text{And, with }\alpha_t = \frac{I_t}{I_0}
\\
\pmb x_t \sim \pmb{\mathcal{N}}(\alpha_t\pmb x_{-1}, \alpha_t\pmb\sigma^2_q +\sigma_e ^2)
\\
\pmb x_t = \alpha_t\pmb x_{-1} + \sqrt{ \alpha_t\pmb\sigma^2_q +\sigma_e ^2}\pmb\epsilon\)
Note that the sampling of $\pmb x_0$ is equivalent if we define $\alpha_0 = 1$, which is true
Continuous Low Dose SDE Derivation
From LDP [Wang 2014], transition between $\pmb x_{t+\Delta t}$ and $\pmb x_{t}$ can be formulated as follows:
\(\text{Define: }\alpha'_t = \frac{\alpha_{t+\Delta t}}{\alpha_t}
\\
\pmb x_{t+\Delta t} = \alpha'_t\pmb x_t + \pmb\sigma_{q,inj}\pmb\epsilon + \sigma_{e,inj}\pmb\epsilon\)
To match the noise vairance for both quantum noise and electronic noise:
\(\begin{equation}
\begin{aligned}
\pmb \sigma_{q,target}^2 = \alpha_{t+\Delta t}\pmb\sigma_q^2
&= {\alpha'_t}^2\pmb\sigma_{q,x_t}^2 + \pmb\sigma_{q,inj}^2
\\
&= {\alpha'_t}^2\alpha_t\pmb\sigma_q^2 + \pmb\sigma_{q,inj}^2
\end{aligned}
\end{equation}
\\
\\\)
\[\begin{equation}
\begin{aligned}
\sigma_{e,target}^2 = \sigma_e^2
&= {\alpha'_t}^2\sigma_{e,x_t}^2 + \sigma_{e,inj}^2
\\
&= {\alpha'_t}^2\sigma_e^2 + \sigma_{e,inj}^2
\end{aligned}
\end{equation}\]
The injected noise variance:
\[\begin{align}
\pmb\sigma_{q,inj}^2 &= (\alpha_{t+\Delta t}- {\alpha'_t}^2\alpha_t)\pmb\sigma_q^2
\\
\sigma_{e,inj}^2 &= (1 - {\alpha'_t}^2)\sigma_e^2
\end{align}\]
Now, we can write the transition from $\pmb x_t$ to $\pmb x_{t+\Delta t}$ as follows:
\(\pmb x_{t+\Delta t} = \alpha'_t\pmb x_{t} + \sqrt{(\alpha_{t+\Delta t}- {\alpha'_t}^2\alpha_t)\pmb\sigma_q^2}\pmb\epsilon + \sqrt{\left(1-\alpha{'}_{t}^{2}\right)}\sigma_e\pmb\epsilon\)
Subtract both sides of $\pmb x_t$
\(\pmb x_{t+\Delta t} - \pmb x_t = (\alpha'_t-1)\pmb x_{t} + \sqrt{\left(\alpha'_t - \alpha{'}_{t}^{2}\right)\frac{\pmb x_{-1}}{I_0}}\pmb\epsilon + \sqrt{\left(1-\alpha{'}_{t}^{2}\right)}\sigma_e\pmb\epsilon\)
For the $\pmb x_t$ term
\[\begin{equation}
\begin{aligned}
(\alpha'_t-1)\pmb x_{t} &= \frac{\alpha_{t + \Delta t} - \alpha_t}{\alpha_t} \pmb x_t
\\ &= \frac{\alpha_{t + \Delta t} - \alpha_t}{\Delta t} \frac{\pmb x_t}{\alpha_t}\Delta t
\end{aligned}
\end{equation}\]
Take limit $\lim_{\Delta t\rightarrow0}$
\(\lim_{\Delta t\rightarrow0}(\alpha'_t-1)\pmb x_{t} = \frac{d\alpha_t}{dt}\frac{\pmb x_t}{\alpha_t}dt\)
For the Quantum noise term
\[\begin{equation}
\begin{aligned}
\sqrt{(\alpha_{t+\Delta t}- {\alpha'_t}^2\alpha_t)\pmb\sigma_q^2}\pmb\epsilon
&=
\sqrt{(\alpha'_t\alpha_t- {\alpha'_t}^2\alpha_t)\pmb\sigma_q^2}\pmb\epsilon
\\&=
\sqrt{\alpha_t\alpha'_t(1- \alpha'_t)\pmb\sigma_q^2}\pmb\epsilon
\\&=
\sqrt{\alpha_t}\sqrt{\alpha'_t(1- \alpha'_t)\pmb\sigma_q^2}\pmb\epsilon
\end{aligned}
\end{equation}\]
\[\begin{equation}
\begin{aligned}
\sqrt{\alpha_t}\sqrt{\alpha'_t\left(1 - \alpha{'}_{t}\right)}
&= \sqrt{\alpha_t}\sqrt{\alpha'_t\frac{\alpha_t - \alpha_{t + \Delta t} }{\alpha_t}}
\\
&= \sqrt{\alpha_t}\sqrt{\frac{\alpha'_t}{\alpha_t}\frac{\alpha_t - \alpha_{t + \Delta t} }{\Delta t}\Delta t}
\\
&= \sqrt{\alpha_t}\sqrt{\frac{\alpha_{t + \Delta t}}{\alpha_t^2}}\sqrt{\frac{\alpha_t - \alpha_{t + \Delta t} }{\Delta t}}\sqrt{\Delta t}
\\
&= \sqrt{\frac{\alpha_{t + \Delta t}}{\alpha_t}}\sqrt{\frac{\alpha_t - \alpha_{t + \Delta t} }{\Delta t}}\sqrt{\Delta t}
\end{aligned}
\end{equation}\]
\[\begin{equation}
\begin{aligned}
\sqrt{(\alpha_{t+\Delta t}- {\alpha'_t}^2\alpha_t)\pmb\sigma_q^2}\pmb\epsilon
&= \sqrt{\frac{\alpha_{t + \Delta t}}{\alpha_t}}\sqrt{\frac{\alpha_t - \alpha_{t + \Delta t} }{\Delta t}}\sqrt{\Delta t}\sqrt{\pmb\sigma_q^2}\pmb\epsilon
\\&=
\sqrt{\frac{\alpha_{t + \Delta t}}{\alpha_t}}\pmb\sigma_q\sqrt{\frac{\alpha_t - \alpha_{t + \Delta t} }{\Delta t}}\sqrt{\Delta t}\pmb\epsilon
\end{aligned}
\end{equation}\]
For the Electronic noise term
\[\sqrt{\left(1-\alpha{'}_{t}^{2}\right)}\sigma_e\pmb\epsilon = \sqrt{(1+\alpha{'}_{t})(1-\alpha{'}_{t})}\sigma_e\pmb\epsilon
\\\]
\[\begin{equation}
\begin{aligned}
\sqrt{(1+\alpha{'}_{t})(1-\alpha{'}_{t})}
&=
\sqrt{(1+\alpha{'}_{t})\frac{\alpha_t - \alpha_{t + \Delta t} }{\alpha_t}}
\\&=
\sqrt{\frac{(1+\alpha{'}_{t})}{\alpha_t}\frac{\alpha_t - \alpha_{t + \Delta t} }{\Delta t}\Delta t}
\\&=
\sqrt{\frac{\alpha_t + \alpha_{t + \Delta t}}{\alpha_t^2}}\sqrt{\frac{\alpha_t - \alpha_{t + \Delta t} }{\Delta t}}\sqrt{\Delta t}
\end{aligned}
\end{equation}\]
\[\begin{equation}
\begin{aligned}
\sqrt{\left(1-\alpha{'}_{t}^{2}\right)}\sigma_e\pmb\epsilon
&=
\sqrt{\frac{\alpha_t + \alpha_{t + \Delta t}}{\alpha_t^2}}\sqrt{\frac{\alpha_t - \alpha_{t + \Delta t} }{\Delta t}}\sqrt{\Delta t}\sigma_e\pmb\epsilon
\\&=
\sqrt{\frac{\alpha_t + \alpha_{t + \Delta t}}{\alpha_t^2}}\sigma_e\sqrt{\frac{\alpha_t - \alpha_{t + \Delta t} }{\Delta t}}\sqrt{\Delta t}\pmb\epsilon
\end{aligned}
\end{equation}\]
Adding equation (13) and (16) together:
\(\left(\sqrt{\frac{\alpha_{t + \Delta t}}{\alpha_t}}\pmb\sigma_q + \sqrt{\frac{\alpha_t + \alpha_{t + \Delta t}}{\alpha_t^2}}\sigma_e\right)\sqrt{\frac{\alpha_t - \alpha_{t + \Delta t} }{\Delta t}}\sqrt{\Delta t}\pmb\epsilon\)
Then take $\lim_{\Delta t\rightarrow0}$:
From Wolframe Alpha $\lim_{a\rightarrow0}\frac{f(x+a)}{f(x)} = 1$ and $\lim_{a\rightarrow0}\frac{f(x+a)+f(x)}{f^2(x)} = \frac{2}{f(x)}$
\(\begin{equation}
\begin{aligned}
\left(\pmb\sigma_q + \sqrt{\frac{2}{\alpha_t}}\sigma_e\right)\sqrt{-\frac{d\alpha_t}{d t}}\sqrt{d t} \pmb \epsilon
&=
\left(\sqrt{\alpha_t}\pmb\sigma_q + \sqrt{2}\sigma_e\right)\sqrt{-\frac{1}{\alpha_t}\frac{d\alpha_t}{d t}}\sqrt{d t} \pmb \epsilon
\end{aligned}
\end{equation}\)
Now, with $\lim_{\Delta t\rightarrow0} \pmb x_{t+\Delta t }-\pmb x_t = d\pmb x$, the whole SDE becomes:
\(\begin{equation}
\begin{aligned}
dx
&= \frac{d\alpha_t}{dt}\frac{\pmb x_t}{\alpha_t}dt +\left(\sqrt{\alpha_t}\pmb\sigma_q + \sqrt{2}\sigma_e\right)\sqrt{-\frac{1}{\alpha_t}\frac{d\alpha_t}{d t}}\sqrt{d t} \pmb \epsilon
\\&=
\frac{A(t)}{\alpha(t)}\pmb x_tdt + \left(\sqrt{\alpha_t}\pmb\sigma_q + \sqrt{2}\sigma_e\right)\sqrt{-\frac{A(t)}{\alpha(t)}}d \pmb w
\\&=
D(t)\pmb x_tdt + \left(\sqrt{\alpha_t}\pmb\sigma_q + \sqrt{2}\sigma_e\right)\sqrt{-D(t)}d \pmb w
\end{aligned}
\end{equation}\)
Where we define
\(\begin{align}
\text{Tube Output Scaling Factor: }\alpha(t) \equiv \alpha_t &= \frac{I_t}{I_0}
\\
\text{Dose Scheduling: }
D(t) &= \frac{A(t)}{\alpha(t)}
\\
d\pmb w &= \sqrt{dt}\pmb\epsilon
\\
A(t) &= \frac{d\alpha(t)}{dt}
\end{align}\)
The final standard SDE from
\[d\pmb x = \pmb f(\pmb x,t)dt + \pmb g(t)d\pmb w\]
Where
\(\begin{align}
\pmb f(\pmb x,t) &= D(t)\pmb x_t
\\
\pmb g(t) &= \left(\sqrt{\alpha_t}\pmb\sigma_q + \sqrt{2}\sigma_e\right)\sqrt{-D(t)}
\end{align}\)
Reverse Low-Dose SDE
Follow the similar derivation in Fourier Diffusion SDE [Tivnan, 2023]
Reverse SDE
\(d\pmb x = \left[\pmb f(\pmb x,t) - \pmb g^2(t)\nabla_{\pmb x_t}\log p(\pmb x_t|\pmb x_{-1})\right]dt + \pmb g(t)d\pmb w\)
The main point is then to approximate the score function $\nabla_{\pmb x_t}\log p(\pmb x_t|\pmb x_{-1})$ with neural network $\pmb s_\theta(\pmb x_t, t)$. However, the important thing is to get the ground truth score function.
Recall that
\(\pmb x_t = \alpha_t\pmb x_{-1} + \sqrt{\alpha_t\pmb \sigma_q ^2+\sigma_e ^2}\pmb\epsilon
\\
\pmb x_t \sim \pmb{\mathcal{N}}(\alpha_t\pmb x_{-1},\alpha_t\pmb \sigma_q ^2+\sigma_e ^2)\)
with $\pmb\sigma = \sqrt{\alpha_t\pmb \sigma_q ^2+\sigma_e ^2}$, score function is
\(\pmb u(\pmb x_t) = \nabla_{\pmb x_t}\log p(\pmb x_t|\pmb x_{-1})=\frac1{p(\pmb x_t|\pmb x_{-1})}\frac{\part p(\pmb x_t|\pmb x_{-1})}{\part\pmb x_t}
\\
p(\pmb x_t|\pmb x_{-1}) = \frac{1}{\pmb\sigma\sqrt{2\pi}}e^{-\frac12(\frac{\pmb x_t - \alpha_t\pmb x_{-1}}{\pmb\sigma})^2}
\\
\frac{\part p(\pmb x_t|\pmb x_{-1})}{\part\pmb x_t} = \frac{-(\pmb x_t - \alpha_t\pmb x_{-1})}{\pmb\sigma^2}p(\pmb x_t|\pmb x_{-1})
\\
\nabla_{\pmb x_t}\log p(\pmb x_t|\pmb x_{-1}) = \pmb u(\pmb x_t) = \frac{ -(\pmb x_t - \alpha_t\pmb x_{-1})}{\pmb\sigma^2}\)
Then, the loss function is
\(\mathcal L(\pmb\theta; \pmb\sigma) = \left|\pmb s_{\pmb\theta}(\pmb x_t,t) + \frac{ (\pmb x_t - \alpha_t\pmb x_{-1})}{\pmb\sigma^2}\right|^2
\\
\mathcal L(\pmb\theta; \pmb\sigma) = \left|\pmb s_{\pmb\theta}(\pmb x_t,t) + \frac{ (\pmb x_t - \alpha_t\pmb x_{-1})}{\alpha_t\pmb \sigma_q ^2+\sigma_e ^2}\right|^2\)
**However, the major problem is that even after the network if fully learned, we still have $\pmb x_{-1}$ term in $\pmb g(t)$ in order to go the reverse SDE.. The solution to this is provided below **
Improved Loss And Removal of Need for $\pmb x_{-1}$
Also, notice that if we expand the score function
\(\nabla_{\pmb x_t}\log p(\pmb x_t|\pmb x_{-1}) = \frac{ -(\pmb x_t - \alpha_t\pmb x_{-1})}{\pmb\sigma^2} = \frac{-(\sqrt{\alpha_t\pmb \sigma_q ^2+\sigma_e ^2}\pmb\epsilon)}{\left(\sqrt{\alpha_t\pmb \sigma_q ^2+\sigma_e ^2}\right)^2} = \frac{-\pmb\epsilon}{\sqrt{\alpha_t\pmb \sigma_q ^2+\sigma_e ^2}} = \frac{-\pmb\epsilon}{\pmb\sigma}\)
Which means, we can train the network to predict $-\pmb\epsilon$ instead, we can also use the prior image $\pmb x_T$ as conditioning
\(\mathcal L(\pmb\theta; \pmb\sigma) = \left|\pmb s_{\pmb\theta}(\pmb x_t,\pmb x_T,t) + \pmb\epsilon\right|^2\)
Once fully trained, we can use the network as follows:
\(\begin{aligned}
\pmb x_{-1}&\approx \pmb x_{T}/\alpha_T
\\
\pmb \sigma_q^2 &= \frac{\pmb x_{-1}}{I_0}
\\
\pmb\sigma &= \sqrt{\alpha_t\pmb \sigma_q ^2+\sigma_e ^2}
\\
\pmb f(\pmb x,t) &= D(t)\pmb x_t
\\
\pmb g(t) &= \left(\sqrt{\alpha_t}\pmb\sigma_q + \sqrt{2}\sigma_e\right)\sqrt{-D(t)}
\\
\nabla_{\pmb x_t}\log p(\pmb x_t|\pmb x_{-1}) &= \frac{-\pmb\epsilon}{\pmb\sigma} \approx \frac{\pmb s_{\pmb\theta}(\pmb x_t,\pmb x_T,t)}{\pmb\sigma}
\\
d\pmb x &= \left[\pmb f(\pmb x,t) - \pmb g^2(t)\nabla_{\pmb x_t}\log p(\pmb x_t|\pmb x_{-1})\right]dt + \pmb g(t)d\pmb w
\end{aligned}\)
Dose Scheduling (Linear)
To obtain the dose scheduling term $D(t)$, we start with
\(I_0 : \text{Inital High Dose}
\\
I_{min} : \text{Target Low Dose}
\\
t \in[0,1]
\\
I_0 \rightarrow I_{min} \text{ is linear of }t
\\
I(t) = (I_{min} - I_0)t + I_0\)
Recall that by definition
\(\alpha(t) = \frac{I(t)}{I_0}
\\
\alpha(t) = \frac{(I_{min} - I_0)t + I_0}{I_0} = 1 + \left(\frac{I_{min}}{I_0}-1\right)t\)
Therefore, by definition of $\Alpha(t)$
\(\Alpha(t) = \frac{d\alpha(t)}{dt} = \left(\frac{I_{min}}{I_0}-1\right)\)
Subsequently,
\(D(t) = \frac{\Alpha(t)}{\alpha(t)} = \frac{\frac{I_{min}}{I_0}-1}{1 + \left(\frac{I_{min}}{I_0}-1\right)t} = \frac{I_{min} - I_0}{I_0 + \left(I_{min}-I_0\right)t}\)